How To Understand Math Formulae?
What is a Formula?
It is a mathematical expression or a statement which establishes a relationship between input and output, used to solve similar problems. Thus, it’s more like a generic principle used for problem solving. It usually comprises of an equal sign (=) or a number of variables (known/unknown terms), numbers related by arithmetic operations.
For example, in a given formula 3x + 2 = y, x is the input variable multiplied by 3, when added to 2 gives the output of y. In order to find the area of rectangle, we use formula: A = l x b, here A is area, l is length and b is breath of a rectangle.
- Usually, a formula comprises of single subject variable, located at the left of equal sign. However, with the power of algebra, a subject could be chosen arbitrarily in accordance to the nature of problem and requirement of solution.
- V= l x w x h, in order to find h, it could be rearranged as: h = V/w x l
Understanding a Foreign Language
The subject of mathematics is primarily based on numbers and symbols, its more like understanding and learning a foreign language; therefore, all the new symbols and scribbles look peculiar and incomprehensible. To understand it thoroughly, one need to understand the symbols, meanings, equations, terminologies in order to memorize and imply them later.
Know and Learn the Formulas
In order to understand or learn the formula, it is preferable to know the process behind the formula or how and why it was derived to its certain form? Knowing the entire reason/process behind a certain formula, helps in memorizing it better. It is important to learn the formula you have studied earlier in order to understand the new stuff which comes your way. It is important to recognize the formula and its usability, the letters/notation if they change in some way.
It is not advisable to reply on formula sheets, registering them in your memory is always better to establish a great command and confidence on them and may strengthen the foundation to learn new concepts faster.
Learn the Conditions of Formulas
For instance, when one is using quadratic equation, knowing it as quadratic formula although it isn’t:
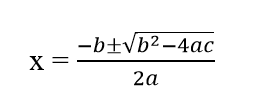
The equation here misses a lot of important information which could help in understanding why it is used. For referring it as quadratic formula, we need to look into all the relevant equations important for its application. Such that:
ax2 + bx + c = 0 derived by the above equation.
Here, a lot of times, the value of ‘x =’ is missed in the quadratic equation, therefore the derived equation and conditions are as important as the quadratic equation to take note of the conceptual understanding behind it! More than most of the exercises in the textbook give the diagrammatic explanation of the practical use of the formula, which could help in understanding the formula through bigger perspective.
Create a Chart of Formulas
Rehearsal is the key to learn mathematics, therefore, taking a view of all the formula you come across in the concepts of your textbooks, the improved familiarity can help in learning and understanding the formula better. Write all the formula with relevant conditions, description in the form of words, photos or graphs can increase the likelihood of overlearning.
Read through the formula everyday no matter if these are needed or not and recall their use and applications.
Identify the Meaning of Formulas
Sometimes, a confusion is built when a simple problem is explained by using different verbal or written jargons such as: the “fraction half” may be written as 1/2, diagonally as ½, as ratio 1:1 or two equal parts and vertically as normal fraction. Similarly, angles can be written in different ways such as in capital letters (A) or in angular form, <BAC, as Greek notations θ, lower-case letters say x, y, or z.
Real-life Implementation of Formulas
Like all other sciences, mathematics is also an important part of our everyday life events, thus, its practical understanding could be developed by looking into the meaning of formula, which concise and symbolic information it holds and for what purpose these have been devised? For instance, there are a number of formulations, through which problems related to construction, engineering, architecture and accounts could be solved. Interestingly, algebraic formula could be used to plan and schedule our daily routine tasks, in computer and medical sciences as well.
Likewise, the formula used in geometry, like area, perimeter, circumference, Pythagoras theorem is also used among different fields. This establish the strong ground to understand the nature and purpose of formula and how through simple x-y equations could resolve the problems in just few minutes, which could otherwise be time-consuming.







