Elementary Results in Random Matrix Theory
Random Matrix
A random matrix is defined as any matric which holds random such as square, correlational or symmetric entries, could be drawn from ‘any number of probability distribution’. A random matrix is simply an N x N matrix in which elements are taken from a N (0,1) distribution, generally with complex eigenvalues.
Eigenvalues are sets of scalar values which are closely related to algebraic linear equations. Generally, the matrix comprise of repeated or complex eigenvalues among which real eigenvalues are more helpful. These matrices are called as Gaussian orthogonal matrices (GOE).
It is clear from the general trend of GOE matrices that as N which is the matrix dimension increases, the general size of the eigenvalues also increases. If average size of eigenvalue is plotted for each N matrix, the proportional relationship is found between eigenvalue scale in size with .
Random Matrix Theory
The Random Matrix Theory (RTM) derives its principles from the statistical mechanics in order to model the complex interactions among complex systems, across the multiple fields related to Mathematics. Initially, it was devised to model the nuclei of heavy atoms which later helped in estimating the covariances in large samples of statistics.
Not only this, the modern applications of this theory are found in theoretical neuroscience, engineering and operations research. A few of the most important empirical results from the random matrix theory are Wigner’s semicircle law, Wigner’s surmise and the Tracy-Widom distribution.
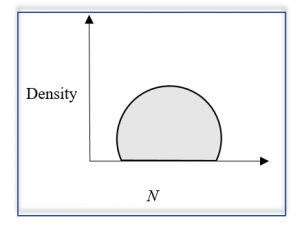
Distribution Of Eigenvalues Of Random Matrices (‘Wigner’s Semicircle’)
In order to generate a large GOE matric of N = 5000, the use of python could plot the distribution of its eigenvalues, generating a semicircle, predominantly known as “Wigner’s semicircle”, resulting from the density of these eigenvalues.
Eugene Wigner, a theoretical physicist gave this law which considered as the most basic result in random matrix theory which demonstrates the non-conformity of eigenvalues to the researcher’s intuition. The eigenvalues scale with is used to normalize each of them by dividing it with 2.
Distribution Of The Spacing Between Eigenvalues (‘Wigner’s Surmise’)
The problem of spacing arises from the doubt of the nature of distribution between two consecutive eigenvalues. By using the similar matrix of 5000 x 5000 matrix, the plotting of the density of spacing between consecutive eigenvalues gives the resemblance of a shifted normal distribution.
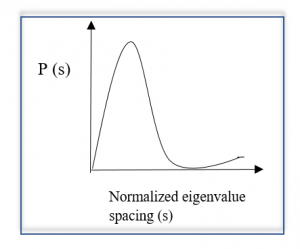
At one conference on neutron physics in 1957, participants were quizzed about the distribution of spacing among the energy levels within the nucleus. Wigner, at that time, came forward and drew a line on the blackboard similar to the above shifted normal distribution, which turned out be incredibly accurate, later named as “Wigner’s surmise”. As a function, Wigner’s surmise could be calculated as:
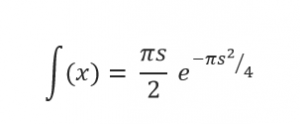
“Wigner’s surmise” explains the phenomenon of ‘level repulsion’ in the terms of quantum mechanics; since particles in their spatial systems have only discrete packets of energy which are called as ‘energy levels or quanta’, generally clustered and sometimes repulsive at a certain distance from each other. The energy levels are at equally distant in which the probability of two coinciding is zero whereas it vanishes when two become s units apart as s increases.
Application in Higher Dimensions
The ideas shared earlier could be generalized into two dimensions to widen the applicability of random matrix theory. “Hermitian matrix” is a complex analogy of a symmetric matrix, which is equal to its own conjugate transpose. For any distribution say N (0,1)2, a and b would be taken from a N (0, 0.5) which would be combined together in the form: sum of a and conjugate b, a + ib.
When all such elements create the sets of “Hermitian matrices”, it is then called as “Gaussian Unitary Ensemble” (GUE). Apart from a few scaling details, GUE matrices also follow “Wigner’s semicircle law” and “Wigner’s surmise”, which helps in studying the complex systems in two dimensions.
Distribution of Largest Eigenvalues of Random Matrices
The common expectation regarding the distribution of the largest eigenvalues that it would be centered at the edge of “Wigner’s semicircle” with some Gaussian noise. However, in 1993, Tracy and Widom introduced the plotting of largest eigenvalues of about 1000 x 1000 matrices for both GOE and GUE resulted in a unique distribution. Unlike “Wigner’s semicircle”, the edge of which appears to be 1, the peak of the “Tracy-Widom distribution” falls slightly below 1 because of computational limitations.
To acquire a function of the form y = f (x), using the numerical approximation is the simplest way, as “Tracy-Widom distribution” is somewhat similar to the gamma distribution. The first three moments of ‘gamma (k, 0) distribution’ are matched with consistent results from data to estimate the parameters.
Twenty years earlier from “Tracy and Widom publication” of their statistical law, a biologist Robert May was interested in modelling the populations of tortoise on an extensive group of islands. The main hypothesis focused on linking the stability of populations of different tortoise species with the number of connections among the islands.
Here, 2 was found at the tipping point which is precisely the peak of “Tracy and Widom distribution”. Later in 1999, some other researchers discover that the “Tracy and Widom Law” also explains the variations in integers which are shuffled, somewhat abstract system strikingly separated from nature.
Hence, it could be concluded that Random Matrix Theory finds its empirical results among a number of dimensions and in different complex systems. An extensive work such as “Wigner’s semicircle law”, “Wigner’s surmise” and “Tracy and Widom Law” have been contributed by the great researchers which was further validated by successive contributions not only in the field of mathematics, but it extended to other fields such as neuroscience, physics, biology and so on.The advance computation such as Python has made the concept of Random Matrix Theory (RTM) much more feasible to comprehend for the modern studies, which acts as a cornerstone for so many significant findings in the given field.







